15. Polar Coordinates

b. Graphs of Polar Equations

4. Intersections of Polar Graphs

Normally, to find the intersection of two graphs, you simply equate the defining functions. However, if two polar graphs intersect at a point \(P\), the coordinates \((r,\theta)\) of the point \(P\) that satisfy one equation may not satisfy the other. It may be necessary to replace the coordinates \((r,\theta)\) in one of the polar equations, by the coordinate \((-r,\theta+\pi)\), which describe the same point, before equating the functions. It may also be necessary to check the origin, since \(r=0\) could correspond to any value of \(\theta\).

Locate all points of intersection of the limacon, \(r=1+2\cos\theta\), and the circle, \(r=1\).

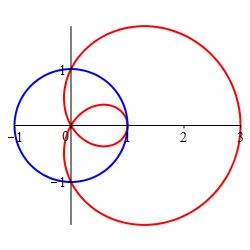
From the graph, we can see three points of intersection, two on the vertical axis and one on the horizontal axis. Let's see if we can find them algebraically. We first equate the two functions: \[\begin{aligned} 1+2\cos\theta=1 \quad &\Rightarrow& \quad &\cos\theta=0 \quad \Rightarrow \\ \theta=\pm\dfrac{\pi}{2},\pm\dfrac{3\pi}{2},\ldots \quad &\Rightarrow& \quad &r=1+2\cos\left(\pm\dfrac{\pi}{2}\right)=1 \end{aligned}\] We obtain only the two intersection points on the \(y\)-axis. We have missed the intersection on the \(x\)-axis. The problem is that the common point on the \(x\)-axis has different coordinates on the two graphs. In fact, this point on the limacon has coordinates \((-1,\pi)\). To find this point, we need to make the substitution \((r,\theta)\;\to\;(-r,\theta+\pi)\) in one of the polar equations.The limacon becomes: \[\begin{aligned} -r&=1+2\cos(\theta+\pi)=1-2\cos\theta \\ \text{or}\qquad r&=-1+2\cos\theta \end{aligned}\] We now equate the two functions: \[\begin{aligned} -1+2\cos\theta=1 \quad &\Rightarrow& \quad &\cos\theta=1 \quad \Rightarrow \\ \theta=0,\pm2\pi,\pm4\pi,\ldots \quad &\Rightarrow& \quad &r=-1+2\cos0=1 \end{aligned}\] This gives the intersection point on the positive \(x\)-axis.

We only need to make the substitution in one graph or the other. And be sure not to make the substitution in both graphs at the same time.

We could alternatively make the substitution \((r,\theta)\;\to\;(-r,\theta+\pi)\) in the circle \(r=1\) to obtain \(r=-1\). If we now equate, we get:

\[\begin{aligned} 1+2\cos\theta=-1 \quad &\Rightarrow& \quad &\cos\theta=-1 \quad \Rightarrow \\ \theta=\pm\pi,\pm3\pi,\pm 5\pi,\ldots \quad &\Rightarrow& \quad &r=1+2\cos(\pi)=-1 \end{aligned}\] This gives the point \((r,\theta)=(-1,\pi)\) which is also the intersection point on the positive \(x\)-axis.

Find all intersections of the polar graphs, \(r=2\sin\theta\) and \(r=2\cos\theta\).

If you only found the intersection at \((r,\theta)=\left(\sqrt{2},\dfrac{\pi}{4}\right)\), you missed a point. Try graphing the two curves.

The graphs intersect at \((r,\theta)=\left(\sqrt{2},\dfrac{\pi}{4}\right)\) and at the origin, \((x,y)=(0,0)\).

We first equate the two equations and solve: \[\begin{aligned} 2\sin\theta=2\cos\theta \quad &\Rightarrow& \quad &\tan\theta=1 \quad \Rightarrow \\ \theta=\dfrac{\pi}{4},\pm\dfrac{5\pi}{4},\ldots \quad &\Rightarrow& \\ r=2\sin\left(\dfrac{\pi}{4}\right)=\dfrac{2}{\sqrt{2}}=\sqrt{2} \quad &\text{or}& \quad &r=2\sin\left(\dfrac{5\pi}{4}\right)=-\sqrt{2} \end{aligned}\] which gives intersections at the points \(\left(\sqrt{2},\dfrac{\pi}{4}\right)\) and \(\left(-\sqrt{2},\dfrac{5\pi}{4}\right)\) which are actually the same point.

Next, we make the substitution \((r,\theta)\;\to\;(-r,\theta+\pi)\) in the second equation to get \(-r=2\cos(\theta+\pi)=-2\cos\theta\) which is equivalent to the original equation \(r=2\cos\theta\). So this does not give any extra intersections.

Finally, we examine the origin. \((r,\theta)=(0,0)\) is a solution of \(r=2\sin\theta\) while \((r,\theta)=\left(0,\dfrac{\pi}{2}\right)\) is a solution of \(r=2\cos\theta\). So the origin, \((x,y)=(0,0)\), is a solution of both equations, although there is no value of \(r\) and \(\theta\) which satisfies both equations!

We check by looking at the graphs.

\(r=2\sin\theta\) is a circle of radius \(1\) centered at \((x,y)=(0,1)\).

\(r=2\cos\theta\) is a circle of radius \(1\) centered at \((x,y)=(1,0)\).

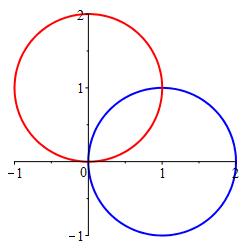
The Moral: Whenever you seek points of intersection of polar graphs, use a graph in conjunction with algebra! Equate the equations, substitute \((r,\theta)\;\to\;(-r,\theta+\pi)\) in one equation and equate them, and check the origin.

15. Polar Coordinates

b. Graphs of Polar Equations

4. Intersections of Polar Graphs

Heading